Sea una planta cuyo comportamiento se modela como un sistema de primer orden. La respuesta de todo el sistema controlado frente a un escalón unitario es la representada en la siguiente figura:

Esta planta es controlada mediante un regulador P, cuya ganancia vale 13.37, y el sistema tiene realimentación unitaria.
Se pide determinar:
- La función de transferencia de la planta.
- Se sustituye el controlador proporcional por uno integral, y en el lazo de realimentación se introduce un sensor cuya ganancia estática es 1.1 y cuya constante de tiempo es 1.02 s. Determinar el máximo valor que puede tomar la ganancia del controlador para que el sistema sea estable.
Respuesta:
Debido a que el sistema se comporta como un sistema de primer grado, podemos suponer que la función de transferencia de dicho sistema es de la forma siguiente:

La constante de tiempo T es el tiempo en que el sistema alcanza un 63.2% de su valor final. De acuerdo con la gráfica de la respuesta del sistema a la entrada escalón unitario, este valor final es de 0.89, por lo tanto, T es el tiempo en que el sistema alcanza el valor de 0.562:

En la gráfica anterior podemos ver que el valor de 0.562 se logra aproximadamente a los 0.36 s. Entonces:

En la función de transferencia predeterminada para el sistema:

La variable a se relaciona con la constante de tiempo T de la manera siguiente:

Para encontrar la constante K debemos considerar que analíticamente la respuesta del sistema a la función escalón es como sigue:

La antitransformada de Laplace de C(s) nos permite obtener c(t):

La ecuación para c(t) nos permite ver que el valor final de la respuesta del sistema es k/a. De la gráfica podemos afirmar entonces que:
 Es decir:
Es decir:

De esta manera podemos afirmar que la función de transferencia del sistema es:

Este resultado lo podemos corroborar con la siguiente simulación:
>> Gs=tf([2.47],[1 2.78]);
>> step(Gs)

La planta es controlada mediante un regulador P, de ganancia k1=13.37, y realimentación unitaria. Ambos componentes se pueden representar mediante el siguiente diagrama de bloque:
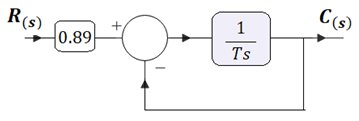
Es decir:

Dónde:

Entonces: De donde:
De donde:
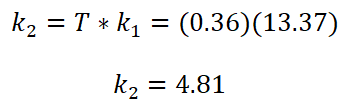
En definitiva, la función de transferencia de la planta es:
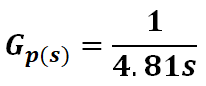
2da parte
Se sustituye el controlador proporcional por uno integral, y en el lazo de realimentación se introduce un sensor cuya ganancia estática es 1.1 y cuya constante de tiempo es 1.02 s. Determinar el máximo valor que puede tomar la ganancia del controlador para que el sistema sea estable.
Respuesta 2:
La nueva situación se representa mediante el siguiente diagrama de bloques:

Dónde:
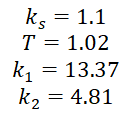
La función de transferencia del lazo realimentado es:
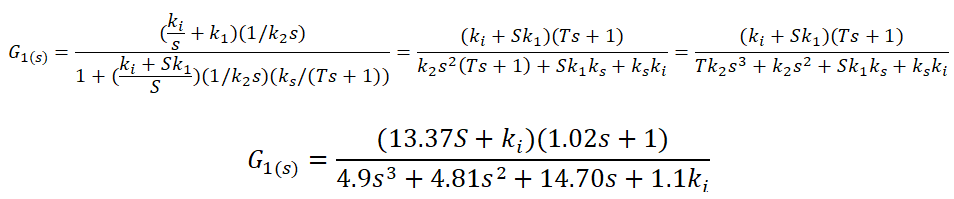
La función de transferencia del sistema en su totalidad es:
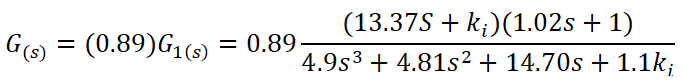
Para estudiar la estabilidad del sistema nos enfocamos en su ecuación característica para aplicar el criterio de Routh-Hurwitz:

Para lograr estabilidad deben cumplir estas dos condiciones:

Del análisis de estabilidad del sistema concluimos que el valor máximo de la constante del controlador integral para garantizar estabilidad es 13.14.
SIGUIENTE:
ADEMÁS:
- La Transformada de Laplace
- Transformada de Laplace del Pulso Rectangular
- La Transformada Z
- La antitransformada de Laplace
- Ejemplo de antitransformada de Laplace
- Ejemplo 1: Transformada de Laplace de una función exponencial – Matlab
- La Función de Transferencia
- La respuesta al impulso, la salida y la integral de convolución de un sist. LIT
- Convolución de señales discretas – Sumatoria de convolución
- Convolución en el tiempo continuo – Ejemplos
- Convolución de un señal con su respuesta al impulso – Ejemplo en Matlab
- Método gráfico de convolución de señales continuas
- Sistemas lineales e invariantes en el tiempo
Escrito por Prof. Larry Francis Obando – Technical Specialist – Educational Content Writer – Twitter: @dademuch
Se hacen trabajos, ejercicios, clases online, talleres, laboratorios, Academic Paper, Tesis, Monografías….Entrega Inmediata !!!…Comunícate conmigo a través de:
- WhatsApp: +34 633129287
- dademuchconnection@gmail.com
Te brindo toda la asesoría que necesites!! …
Mentoring Académico / Emprendedores / Empresarial
Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.
Contacto: Jaén – España: Tlf. 633129287
Caracas, Quito, Guayaquil, Lima, México, Bogotá, Cochabamba, Santiago.
WhatsApp: +34 633129287

2 comentarios en “FT a partir de la respuesta al escalón unitario de un sistema de primer orden”