La ecuación de Bernoulli permite iniciar el estudio de la dinámica de fluidos, especialmente aquellos fluidos que se mueven a través de conductos y tubos.
Por estar basada en el principio de conservación de energía, la ecuación de Bernoulli es a su vez la herramienta fundamental para tomar en cuenta los tres tipos de energías presentes en todo sistema: energía cinética, energía potencial y flujo de energía.
El objetivo de este paper aprenderemos analizar el comportamiento y rendimiento de sistemas de flujo de fluidos. Se trata de adquirir los fundamentos para analizar y diseñar sistemas para transportar ciertas cantidades de fluido desde el punto de fuente hasta el destino deseado.
Es común utilizar tres medidas para el flujo de fluidos: el flujo volumétrico Q; el flujo en peso W; y el flujo másico M. Aprenderemos a relacionar estos términos uno con otro en puntos distintos de un sistema por medio del Principio de Continuidad.
Tasa de flujo de un fluido
El flujo turbulento es muy difícil de estudiar. Por consiguiente, sólo consideramos el flujo no turbulento en estado estacionario, o “flujo ideal”, no viscoso. Es decir, uno que fluye sin disipación de energía mecánica.
La cantidad de flujo que pasa por un sistema por unidad de tiempo puede expresarse por medio de tres términos distintos. El más importante es El flujo volumétrico Q:
1) El flujo volumétrico Q es el volumen de fluido que circula en una sección por unidad de tiempo. Se calcula mediante la siguiente fórmula:
Dónde A es el área de la sección y v es la velocidad promedio del flujo.
La magnitud Av se denomina Caudal Iv. Las dimensiones de Iv son las de volumen dividido por tiempo.
2) El flujo en peso W es el peso del fluido que circula en una sección por unidad de tiempo. Se relaciona con Q por medio de la siguiente ecuación:
Dónde ϒ es el peso específico del fluido.
3) El flujo másico M es la masa de fluido que circula en una sección por unidad de tiempo. Se relaciona con Q por medio de la siguiente ecuación:
Dónde ρ es la densidad del fluido.
El método de cálculo de la velocidad de flujo en un sistema de ductos cerrados depende del Principio de Continuidad. En la Figura 1, un fluido circula con un flujo volumétrico constante desde la sección 1 a la sección 2.
Es decir, la cantidad de flujo que circula a través de cualquier sección en cierta cantidad de tiempo es constante. Esto se conoce como flujo estable. Entonces, se cumple que:
Pero sabemos que:
Por tanto, la ecuación (4) se puede reescribir como:
La ecuación (5) es de gran importancia y se denomina Ley de Continuidad. Como puede verse, relaciona densidad de flujo con área de flujo y velocidad de flujo, y es válida para todos los fluidos, ya sean gases o líquidos. Si el fluido en el tubo de la Figura 1 es un líquido incompresible, entonces los términos y son iguales, por lo que la ecuación (5) se convierte en:
Es decir, la ecuación (6) nos indica que:
Conservación de la energía – Cantidad de energía total.
En el análisis del problema de tuberías de la Figura 1 se toma en cuenta toda la energía dentro del sistema. En Física aprendimos que la energía no se crea ni se destruye, sólo se transforma de una forma en otra. Éste es el enunciado de la Ley de Conservación de Energía.
Se consideran tres tipos de energía en el sistema de la Figura 1:
- Energía Potencial :
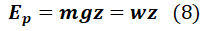
Dónde m es la masa del elemento, g es la gravedad y z es la altura del elemento sobre el nivel de referencia. El peso w del elemento es:
- Energía Cinética :
- Energía de flujo :
En la Figura 1 la fuerza F sobre el elemento es:
Donde P es la presión en la sección de área A. La fuerza F recorre una distancia L igual a la longitud del elemento. Por tanto, el trabajo que realiza es:
Por tanto, utilizando la ecuación (9):
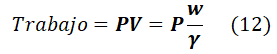
La ecuación (12) es la energía de flujo y es la demostración de la ecuación (11).
Entonces, la cantidad de energía total que posee el elemento de fluido es la suma de E:
Sustituyendo las ecuaciones (8), (10) y (11) en (13), obtenemos:
Cada uno de los términos de la ecuación (14) se expresa en unidades de energía como Newton-metro (N.m).
Ecuación de Bernoulli - El flujo de los Fluidos
Consideramos de nuevo el elemento de la Figura 1:
Los valores de P, z y v son diferentes en las dos secciones. Utilizando la ecuación (14) podemos determinar la energía total en la sección 1 mediante:
Mientras que en la sección 2, la energía total es:
Si no hay energía que se pierda entre las secciones 1 y 2, entonces el principio de conservación de energía requiere que:
Es decir:
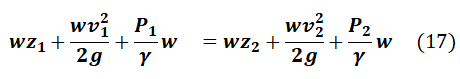
En la ecuación (17) podemos ver que el factor es común a todos los términos, por lo que dicha ecuación se reduce a:
La ecuación (18) es conocida como La ecuación de Bernoulli.
Ya que:
La ecuación (18) se puede escribir como:
Procedimiento para utilizar Bernoulli.
- Determinar cuáles son las dos secciones del sistema que se utilizarán para escribir la ecuación. Una de ellas se elige porque se concentran varios datos conocidos. En la otra, por lo general, está la variable que es solicitada.
- Escribir la ecuación para ambas secciones. Importante es que la ecuación se escriba en la dirección del flujo. Es decir, el flujo debe proceder de la ecuación de la izquierda y dirigirse a la ecuación de la derecha.
- Es imprescindible ser explícito en la denominación de los subíndices de los términos de la carga de presión, la carga de elevación y la carga de velocidad. En un dibujo, es necesario ubicar los puntos de referencia.
- Simplificar y despejar algebraicamente. Sustituir valores.
Ejemplos
1) Suponga que la sangre fluye a través de una aorta de 1.0 cm de diámetro a una velocidad promedio de 50 cm / s. Deje que la presión media en la aorta sea de 100 mmHg. Si la sangre entrara en una región de estenosis donde el diámetro de la aorta es de solo 0.5 cm. ¿Cuál sería la presión aproximada en el sitio de estrechamiento? (Suponga que la densidad sanguínea es de 1.056 g / cm3 y descuide la fricción y efectos de gravedad).
Utilizamos la ecuación de Bernoulli (19) y la ecuación de continuidad (6):
Despejamos P2 de la ecuación (a) y a v2 de la ecuación (b):
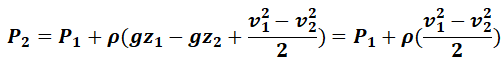
Donde ρ es densidad del elemento. Entonces:
Dónde:
Por tanto:
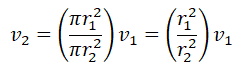Por otra parte:
Entonces:
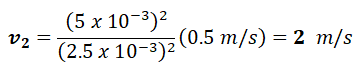Luego:
2) En el ejercicio de la Figura siguiente, hallar Vf, Pa, Pb, Pc, Pd, Pe.
El primer paso para resolver este problema es aplicar la ecuación de Bernoulli en los puntos más convenientes. ¿Cuáles son?
Para hallar Vf
A y F son los puntos más convenientes porque: en A la superficie está libre y sometida a la atmósfera, o sea, Pa=0. La velocidad de la superficie es casi cero, por ello va=0. El punto F es la corriente libre del agua, expuesta a la presión atmosférica, por lo que Pf=0. También sabemos que F está 3.0 m por debajo de A. Entonces:
De donde:
Para hallar Pb
A y B son los puntos más convenientes porque: Ya sabemos que en el punto A se simplifica la ecuación, mientras que en el punto B está la variable de interés. Así obtenemos:
Para hallar Pc
A y C son los puntos más convenientes porque: Ya sabemos que en el punto A se simplifica la ecuación, mientras que en el punto C está la variable de interés. Por otra parte, el área de B es igual al área de C. Así obtenemos:
Para hallar Pd
B y D son los puntos más convenientes porque: la elevación y la velocidad de ambos puntos son iguales. Por ello:
Para hallar Pe
A y E son los puntos más convenientes porque: la elevación y la velocidad de ambos puntos son iguales. Por ello:
Fuentes:
Mecánica de Fluidos – Robert Mott – 6ta. E.
Apuntes de Mecánica de Fluidos II
Apuntes de Mecánica de Fluidos
Física Tipler 5ta Edición Vol 1
Escrito por Prof. Larry Francis Obando – Technical Specialist – Educational Content Writer – Twitter: @dademuch
Se hacen trabajos, ejercicios, clases online, talleres, laboratorios, Academic Paper, Tesis, Monografías….Entrega Inmediata !!!…Comunícate conmigo a través de:
- WhatsApp: +34 633129287
- dademuchconnection@gmail.com
Te brindo toda la asesoría que necesites!! …
Mentoring Académico / Emprendedores / Empresarial
Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.
Contacto: Jaén – España: Tlf. 633129287
Caracas, Quito, Guayaquil, Jaén.
WhatsApp: +34 633129287
FACEBOOK: DademuchConnection
email: dademuchconnection@gmail.com