Ejemplo 1 – Diseño de un controlador PI (Proporcional-Diferencial)

Para apreciar mejor el efecto del controlador PI, veamos el siguiente ejemplo. Supongamos que tenemos el sistema de la Figura 7-23.

La función de transferencia directa G(s) de este sistema viene dada por la siguiente expresión: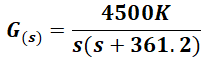

Donde K es la constante del preamplificador.

Las especificaciones de diseño para este sistema son las siguientes:

Donde:

• ess: Error en estado estable debido a una entrada parábola
• Mp: Sobrepaso máximo
• Tr: Tiempo de levantamiento
• Ts: Tiempo de asentamiento

Lo primero que vamos a hacer es analizar el error en estado estable ess del sistema antes de compensar, y ver que tanto cumple o no con el primer requerimiento de diseño (Para un repaso de este tema ver: Error en estado estable de un sistema de control).

Para una entrada parabólica debemos trabajar con la constante de aceleración Ka:Esto significa un error infinito para una entrada parabólica:Para mejorar el error en estado estable incorporamos un controlador PI en la trayectoria directa del sistema, el cual ahora tendrá la siguiente función de transferencia:Al aumentar la tipología del sistema de tipo 1 a tipo 2 de inmediato mejoramos el error en estado estable. Ahora, el ess debido a la entrada parábola será una constante:Es decir:

Este ejercicio ya lo trabajamos con el controlador PD. Para ese caso seleccionamos un valor de K=181.17 (Ejemplo 1 – Diseño de un controlador PD (Proporcional-Diferencial) – Matlab)

Nos permitimos la libertad de considerar el mismo valor para K en este caso con el fin de mantener la respuesta transitoria bajo condiciones aceptables y conocidas al aplicar el PD del ejemplo 1. De ser necesario ajustaremos el valor de K más adelante. Podemos apreciar que para lograr un ess según se especifica en el diseño, mientras más grande sea K, más pequeño tendrá que ser Ki, algo que puede ser conveniente. Con los valores de K y ess podemos calcular un primer valor aproximado de Ki para cumplir con los requerimientos:

Lo siguiente que haremos será analizar la estabilidad del sistema debido a que de ello depende enormemente la selección de los parámetros Kp y Ki. Aplicaremos el criterio de Routh-Hurwitz (para un repaso ver Estabilidad de un sistema de control) para calcular los valores límites de los mencionados parámetros de manera tal que el sistema permanezca estable. Para ello requerimos de la ecuación característica que surge de la función de transferencia del sistema en lazo cerrado Gce(s):

La ecuación característica del sistema es:

Con esta ecuación aplicamos el criterio de Routh-Hurwitz. De esta manera descubrimos que el sistema es estable para el siguiente rango de valores:

Este resultado indica que el Ki/Kp del controlador no puede estar muy cerca del cero, por lo que no resulta conveniente un valor tan bajo tal como Ki=0.002215. Otro criterio para seleccionar Ki/Kp es que resulta conveniente seleccionar el cero añadido por el controlador en s=-Ki/Kp para que esté localizado cerca del origen y lejos de los polos más significativos del sistema. Mediante el lugar geométrico de las raíces en Matlab podemos ver cuáles son los polos más significativos de la ecuación característica, suponiendo una relación aceptable entre los parámetros Ki y Kp desde el punto de vista del estudio de estabilidad anterior pero relativamente cerca del origen, digamos Ki/Kp=10, manteniendo Ki constante y variando Kp (Para un repaso del tema ver: El lugar geométrico de las raíces con Matlab) Primero, arreglamos la ecuación característica en su forma 1+G(s)H(s):

Notar que de esta manera el controlador PI está añadiendo un zero en s=-10.

Aplicamos el siguiente comando en Matlab para obtener el lugar geométrico de las raíces de este sistema compensado:

>> s=tf(‘s’)

>> sys=(815265*(s+10))/(s^3+361.2*s^2)

>> rlocus(sys)

Y obtenemos:

Como se puede observar, el polo más significativo de la ecuación característica está ubicado en s=-361. Por tanto, el criterio que debemos utilizar para seleccionar s=-Ki/Kp es:Con este resultado, la función de transferencia directa G(s):Quedaría simplificada como:

El término Ki/Kp sería despreciable comparado con la magnitud de s cuando s asume valores a lo largo del lugar geométrico de las raíces que se corresponde con un factor de amortiguamiento relativo conveniente de 0.7<ζ< 0.1. Luego, un zero en cero anula un polo en cero. El sobrepaso máximo debe ser igual o menor al 5%. Esto significa que se desea un factor de amortiguamiento relativo ζ aproximado al siguiente valor:

Con la ayuda del lugar geométrico podemos ubicar los polos que se corresponden con este valor de ζ:

De acuerdo con la gráfica, el valor de Kp requerido para obtener este factor de amortiguamiento es:

Y por tanto:

También observamos en la gráfica anterior que si Kp=0.0838, entonces las raíces de la ecuación característica (los polos del sistema) están en s1=-175+j184 y en s2=-175-j184 Si miramos alrededor de esas raíces podemos notar que el zero añadido por el controlador en s=-10 está muy cerca del origen comparado con los polos de s1 y s2, prácticamente cancelando un polo en el origen, ratificando así la aproximación que hicimos anteriormente para la función de transferencia directa de este sistema luego de la compensación:

Así:

Podemos observar la respuesta del sistema al escalón unitario de acuerdo con estos resultados parciales y la comparación de los sistemas compensado y sin compensar, mediante la siguiente simulación:

>> Ga=(815265)/(s*(s+361.2))

>> Gd=(68319)/(s*(s+361.2))

>> Gce1=feedback(Ga,1)

>> Gce2=feedback(Gd,1)

>> step(Gce1,Gce2)

La gráfica anterior, con el sistema después de la compensación en línea roja, muestra que el PI mejora el error en estado estable y reduce el sobrepaso, pero a expensas de aumentar significativamente el tiempo de levantamiento. La gráfica también nos muestra que el sobrepaso máximo es de 5%, por tanto se cumple el requerimiento. Es necesario notar que se puede seleccionar otra relación para Ki y Kp que cumpla con el requerimiento y aún mejoren el sobrepaso, por ejemplo Ki/Kp=5, o Ki/Kp=2. Sólo hay que prestar atención al tema de la estabilidad del sistema. Con los valores calculados, volvemos a calcular el sobrepaso, y vemos como quedan el tiempo de levantamiento tr y el tiempo de asentamiento ts. El siguiente comando nos facilita el valor de ζ y ωn, el factor de amortiguamiento relativo y la frecuencia natural respectivamente (Para un repaso ver:Respuesta Transitoria de un Sistema de Control).

>> damp(Gce2)

Pole: -1.81e+02 + 1.89e+02i /   -1.81e+02 + 1.89e+02i

Damping: 6.91e-01

Frequency: 2.61e+02

•  Máximo Sobrepaso (MP):

• Tiempo de levantamiento (Tr):

>> Gd=(68319)/(s*(s+361.2))

>> sys=feedback(Gd,1)

>> step(sys)

• Tiempo de asentamiento (Ts):

Cosa que también podemos constatar en la gráfica de respuesta al escalón unitario generada anteriormente:

Podemos concluir que el sistema compensado cumple con los requerimientos del diseño, aunque se sobrepasa un poco en el tiempo de asentamiento. Este último se puede reducir levemente con una relación Ki/Kp=2, pero a expensas de acercarse demasiado a la zona inestable del sistema.

ANTERIOR: PID – Diseño con el controlador PD (Proporcional-Diferencial)

Escrito por: Larry Francis Obando – Technical Specialist – Educational Content Writer.

Mentoring Académico / Empresarial / Emprendedores

Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)

Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, Valle de Sartenejas

Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, Caracas.

Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.

Contact: España, Caracas, Quito, Guayaquil, Cuenca –

WhatsApp: +34633129287

email: dademuchconnection@gmail.com

Atención: Si lo que Usted necesita es resolver con urgencia un problema de “Sistema Masa-Resorte-Amortiguador” (encontrar la salida X(t), gráficas en Matlab del sistema de 2do Orden y parámetros relevantes, etc.), o un problema de “Sistema de Control Electromecánico” que involucra motores, engranajes, amplificadores diferenciales, etc…para entregar a su profesor en dos o tres días, o con mayor urgencia…o simplemente necesita un asesor para resolver el problema y estudiar para el próximo examen…envíeme el problema…Yo le resolveré problemas de Sistemas de Control, le entrego la respuesta en digital y le brindo una video-conferencia para explicarle la solución…incluye además simulación en Matlab.

Relacionado:

Respuesta Transitoria de un Sistema de Control

Estabilidad de un sistema de control

Simulación de Respuesta Transitoria con Matlab – Introducción